Density Functional Theory (DFT) has been widely used in the fields of condensed matter physics, materials science, quantum chemistry and life sciences as an approximation method for dealing with multi-particle systems. For example, Figure 1(c) is a 72-atom supercell structure calculated using the DFT method [1]. The DFT-based material science computational simulation method can not only study existing materials, but also predict new materials.
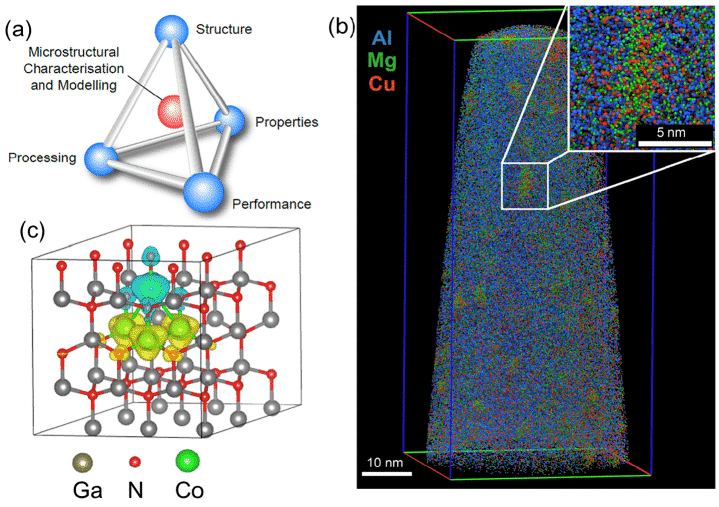
figure 1 (a) Potential link between microscopic characterization, structure, processing, properties and properties, (b) APT data for Al-Cu-Mg alloys containing approximately 20 million atoms, (c) 72-atom for DFT calculations Supercell example
A functional is a mapping from vector space to scalar, a function of a function. Table 1 lists some of the types of density functionals that have been proposed, some of which are derived from basic quantum mechanics and some that are derived from parametric functions, each with its own advantages and disadvantages and scope of application [2]. The essence of the DFT method is to use the electron density as the carrier of all the information in the molecular (atomic) ground state, rather than the wave function of a single electron, so that the multi-electron system can be transformed into a single electron problem. Assuming that the number of electrons is N, the number of variables in the wave function is 3N, and the density functional theory reduces the number of variables to three spatial variables, which simplifies the calculation process and ensures the calculation accuracy.
Table 1 Some approximate density functional types

The development of density functional theory can be roughly divided into three stages. The first stage was in 1927. Thomas and Fermi proposed the Thomas-Fermi model based on the ideal electronic gas hypothesis under ideal conditions. For the first time, the concept of density functional theory was introduced, which became the prototype of the later DFT method.
The starting point of the Thomas-Fermi model is to assume that there is no interaction between electrons and no external interference, then the Schr?dinger equation for electron motion can be expressed as:
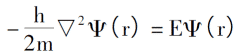
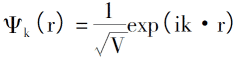
Introducing the law of electron arrangement under 0K, the electron density, the total energy of single electrons and the kinetic energy density of the system are:
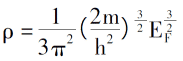
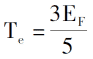
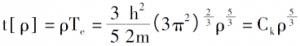
By introducing a description of the coulomb potential and the external field between electrons, the total energy expression of the electronic system determined only by the electron density function can be derived [3].
Although the model simplifies the calculation form and process, it does not consider the interaction between electrons. It does not accurately describe the kinetic energy items, so it is not applicable in many systems. However, inspired by this novel research idea, the relevant scholars have basically perfected the content of density functional theory in the 1960s after many years of efforts, and finally established a strict density functional theory.
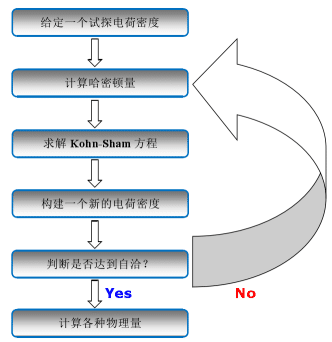
Figure 2 Schematic diagram of a self-consistent iterative process based on DFT
The Hohenberg-Kohn theorem and the Kohn-Sham equation have played a key role in the formation and improvement of the DFT method, and have been hailed as the two cornerstones of DFT.
(1) Hohenberg-Kohn theorem
The core idea of the Hohenberg-Kohn theorem is that all the physical quantities in the system can be uniquely determined by variables containing only electron density, and the implementation method is to obtain the ground state of the system through the variational principle. This theory is mainly for the non-uniform electron gas model and consists of two sub-theorems. i) an electron system that ignores spin at the external potential (potential other than the electronic interaction) whose external potential can be determined by electron density uniquely; ii) for a given external potential, the system ground state energy is the minimum of the energy functional value. Thus, the energy functional of the system can be described as:
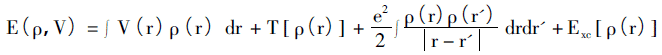
The right side of the equation is the potential energy, the kinetic energy term, the coulomb interaction between electrons, and the exchange-related potential energy in the external field.
This theorem does not give specific expressions of electron density function, kinetic energy functional and exchange-related functional, so the specific solution is still not possible.
(2) Kohn-Sham equation
Until 1965, Kohn and Shen Lujiu established the Kohn-Sham equation, giving a detailed description of each item, and the density functional theory began to enter the practical application stage. They proposed for the kinetic energy functionals to use the particle kinetic energy functionals without interaction to approximate the substitution, and the differences between the two are included in the unknowns of the exchange-related functionals [4].The variation of ρ is replaced by the variation of Φi(r), and the Lagrange multiplier is replaced by Ei. The single electron equation is:
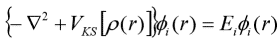
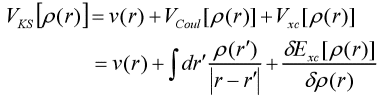
The above is the Kohn-Sham equation.
The Kohn-Sham equation gives a clear expression to everything outside the exchange-associated functional, and also categorizes complex effects into this term. At this point, the computational difficulty is greatly simplified, and all the work begins around how to describe the exchange-related functional expansion. At the same time, the approximate form of the exchange-related potential also directly determines the accuracy of the density functional theory.
The Local Density Approximation (LDA) method was also proposed by Kohn and Shen Lujiu in 1965. The purpose is to approximate the unknown exchange associations, so that the DFT method can be used for actual calculation. LDA uses the density function of uniform electron gas to calculate the exchange relation of non-uniform electron gas. Assuming that the electron density in the system changes very little with space, the exchange relation of non-uniform electron gas can be expressed as:
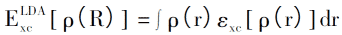
The corresponding exchange correlation potential can be expressed as:
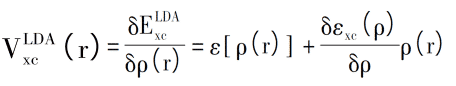
For example, Asad Mahmood et al. used VASP to compare the equilibrium structural parameters of LDA-PBE and GGA-PAW calculations, and studied the effects of Ga doping on electron orbital hybridization, as well as optical properties and crystal geometry, from Figure 3(c). It can be seen that the Ga-2s and Ga-2p orbitals contribute significantly to the conduction, the lower VB also contributes by Ga-2p, and the impurity band at the bottom of the CB suggests an additional energy barrier, the electron between VB and CB. The transition must cross the energy barrier [5].
Figure 3 Calculation results
(a) Optimized 3x3x3 Ga-doped ZnO supercell, (b) band structure, (c) density DOS
In order to calculate the actual material system more accurately, in 1986, Becke, Perdew, and Wang et al. proposed Generalized Gradient Approximation (GGA), which is the most widely used processing method in density functional calculation.
The GGA processing method is to rewrite the original representation into a functional form containing electron density and gradient functions, plus a description of the spin, and the resulting exchange-related functional is as follows:
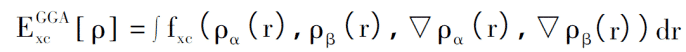
In GGA, the exchange correlation potential can also be disassembled into exchange energy and correlation energy. So how do you construct a reasonable expression for these two parts? Beckc et al. believe that the concrete functional form can be constructed arbitrarily in principle, and does not need to consider the actual physical meaning, such as GGA-PW91; while Perdew et al. advocates returning to pure quantum mechanical calculation theory as much as possible, all physical quantities are only calculated. Starting from basic constants such as electronic static mass, Planck’s constant, and speed of light, functional expressions should not contain excessive empirical parameters, such as GGA-PBE (Perdew-Burke-Enzerhoff), which is often used in fields such as condensed matter physics.
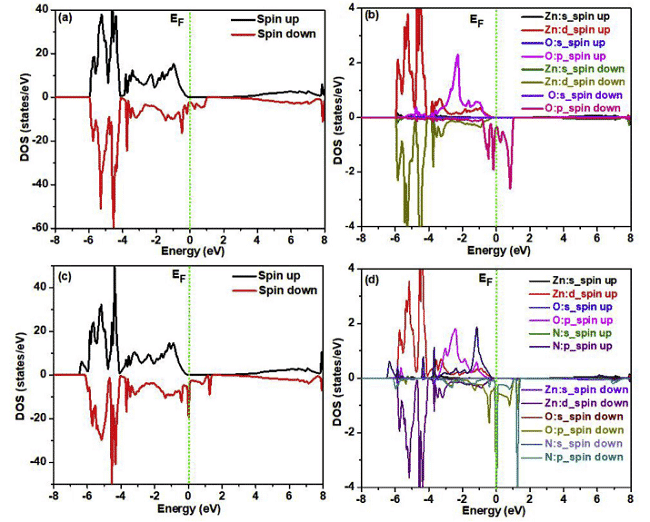
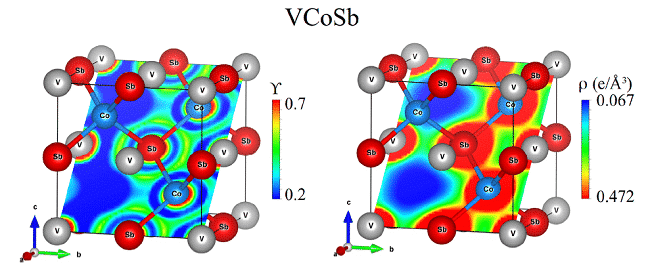
Recently, Parmod Kumar and L. Romaka et al. carried out related research using FP-LAPW (full potential linearly enhanced plane wave) in WIEN2k and Elk v2.3.22, respectively, in which the exchange correlation potential is in the form of GGA-PBE, Figure 4, 5 Calculated results for the corresponding density of states and charge density distribution [6,7].
Fig. 4 Total density of states and local density of states of spin-polarized ZnO super-cells without N injection and implantation
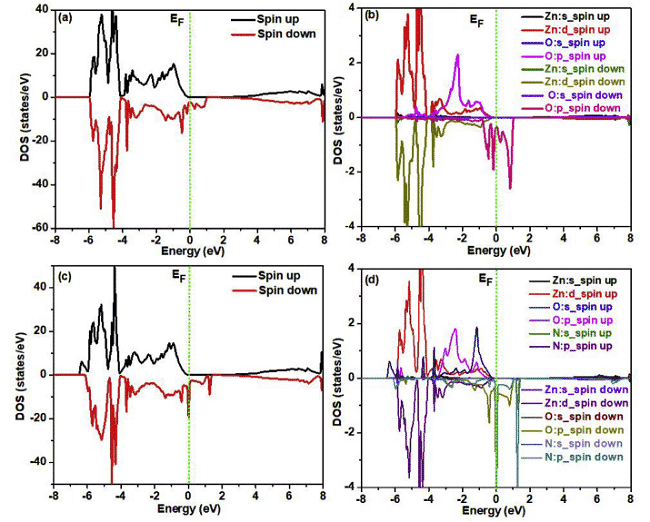
Fig. 5 Distribution of electron localization function (Y) and charge density (r) in VCoSb telluride J. Ibá?ez, T. Wo?niak et al. tested the validity of different density functional theory to predict the lattice dynamics of HfS2 under pressure.
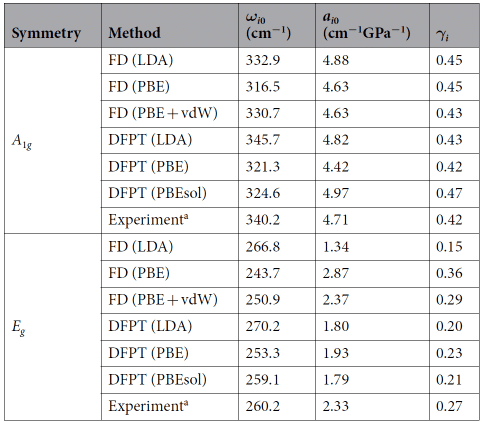
Observation Table 2 found that GGA-DFT properly describes the high-pressure lattice dynamics of HfS2 considering vdW interaction, while LDA-DFT calculation is widely used to predict the structure and vibration characteristics of 2D compounds under environmental conditions, and cannot be reproduced under compression conditions. The behavior of HfS2, which indicates that using DFT-LDA to calculate the compressibility of the TMDCs and the Grüneisen parameters will produce large errors [8].
Table 2 Raman frequency (ωi0), pressure coefficient (ai0) and Grüneisen parameter (γi)
In addition to the LDA and GGA algorithms, there are also hybrid density functionals that incorporate Hatree-Fock (HF) exchange effects into the exchange associations in a hybrid manner, such as B3LYP, which was popular in 1998. These theories contain more and more systematic information, and the calculation results are getting closer and closer to the experimental data, especially suitable for the field of organic chemistry, and have achieved great success in the calculation of chemical reaction mechanism.
For example, T. Garwood et al. calculated the bandgap data of the InAs/GaSb II type superlattice structure (model shown in Figure 6) using PBE0 type hybridization [9], which is very close to the experimental value, and the deviation range is about 3 %-11%.
Figure 6 Ball-and-stick InAs / GaSb SLS model of hybrid DFT calculated using VESTA
The electron band structure theory based on Kohn-Sham single-particle energy spectrum can qualitatively describe many materials, but it is not satisfactory from a quantitative point of view. For example, for simple semiconductor materials such as Si and GaAs, the band gap given by the Kohn-Sham DFT under LDA/GG is much smaller; for small bandgap semiconductors such as Ge and InN, the metal obtained from LDA/GGA is metal. State, but the experimental observation is semiconductor, which is the so-called LDA / GGA band gap problem.
In order to overcome the band gap problem, people have made a lot of efforts in the theoretical framework of DFT, such as extending the Kohn-Sham theory based on local effective potential to the Generalized Kohn-Sham (GKS) theory based on non-local effective potential, and Other hybrid density functional theory, there is a multi-body perturbation theory based on the one-body Green’s function. In this theory, the exchange-related potential with the Kohn-Sham DFT corresponds to the exchange-associated self-energy operator. For the self-energy operator, a relatively simple and accurate approximation is the GW approximation (the product of the single-particle Green’s function G and the shielded Coulomb effect W). By calculating the self-energy operator under a certain approximation, we can get the corresponding PES (IPS). The quasi-particles in the excitation energy. Although these new development directions have improved the description of the band gap of materials, the approximate functionals still have great subjectivity, and the scope of application is relatively limited. So far, there is not a universal DFT method with sufficient theoretical basis. An accurate description of the material’s electronic band structure [10,11].
In addition, there are some extensions based on the existing density functional theory. For example, the time-dependent density functional theory (TDDFT) based on the KS orbital energy difference is used to replace the Schordinger equation with the single-particle Dirac equation. The density density functional theory extends to LDA+U of strong correlation systems and the flow density functional theory (CDFT) for dealing with interacting electron systems under arbitrary magnetic fields.
Referanslar
Xiang-Yuan Cui, Simon P. Ringer,On the nexus between atom probe microscopy and density functional theorysimulations [J] ,Materials
Characterization (2018), https://doi.org/10.1016/ matchar.2018.05.015
B. Obot, D.D. Macdonald, Z.M. Gasem,Density functional theory
(DFT) as a powerful tool for designing neworganic corrosion inhibitors. Part 1: An overview [J],Corrosion Science 99 (2015) 1–30
Geerlings, F. De Proft, W. Langenaeker, Conceptual density functional theory,Chem. Rev. 103 (2003) 1793–1873.
Nagy, Density functional theory and application to atoms and molecules, Rev. 298 (1998) 1–79.
Koch, M.C. Holthausen, A Chemist’s Guide to Density Functional Theory,Wiley-VCH, Weinheim, 2000.
Asad Mahmood, Fatih Tezcan, Gulfeza Kardas,Thermal decomposition of sol-gel derived Zn0.8Ga0.2O precursor-gel: Akinetic, thermodynamic, and DFT studies [J],Acta Materialia 146 (2018) 152-159
Parmod Kumar, Hitendra K. Malik, Anima Ghosh, R. Thangavel, K. Asokan,An insight to origin of ferromagnetism in ZnO and N
implanted ZnOthin films: Experimental and DFT approach [J],Journal of Alloys and Compounds 768 (2018) 323-328
Romaka, V.V. Romaka, N. Melnychenko, Yu. Stadnyk, L. Bohun, A. Horyn,Experimental and DFT study of the VeCoeSb ternary system[J] ,Journal of Alloys and Compounds 739 (2018) 771-779
Ibá?ez, T. Wo?niak, F. Dybala, R. Oliva, S. Hernández,R. Kudrawiec,High-pressure Raman scattering inbulk HfS2: comparison of density functional theory methods in layered MS2 compounds (M = Hf, Mo) under compression [J],Scientific reports (2018) 8:12757,DOI: 10.1038/ s41598-018-31051-y
Garwood, N.A. Modine, S. Krishna,Electronic structure modeling of InAs/GaSb superlattices with hybriddensity functional theory [J],Infrared Physics & Technology 81 (2017) 27–31
Eugene S. Kryachko, Eduardo V. Ludena,Density functional theory: Foundations reviewed[J],Physics Reports 544 (2014) 123–239
B. Obot, D.D. Macdonald, Z.M. Gasem,Density functional theory (DFT) as a powerful tool for designing neworganic corrosion inhibitors. Part 1: An overview [J],Corrosion Science 99 (2015) 1–30









