In order for the microscopic simulation system to reflect the macroscopic experimental phenomena, it is necessary to periodically replicate the simulated object system through periodic boundary conditions to avoid edge effects that do not exist in practice. In principle, the theoretical study of any molecular system requires the solution of the time-dependent Schr?dinger equation. However, in practice, more attention is paid to the trajectory of the nucleus. Such a trajectory can be obtained by solving the classical mechanical equation of motion using the Born-Oppenheimer approximation. Alder and Wainwright have said that computer simulation experiments will become an important bridge connecting macroscopic experimental phenomena and microscopic nature. After 10 years of their first molecular dynamics simulation experiments, French physicist Verlet proposed an integration algorithm for Newton’s equations of motion. At the same time, another set of algorithms for generating and recording pairs of neighboring atoms is proposed, which greatly simplifies the calculation of the interaction between atoms. These two algorithms are still widely used in practice in some variants [1, 2].
A variety of atomic-level simulation methods have been developed over the past few decades, including lattice statics, lattice dynamics, Monte Carlo, and molecular dynamics. Among them, molecular dynamics is especially suitable for the study of plastic deformation. It studies the real-time behavior of deformation process through the solution of Newton’s equation of the atomic interaction system of some defined interatomic interaction potential functions, and includes the non-simplification of the lattice. Harmonicity, height unevenness of internal stress, and transient response of the system.
Molecular dynamics mainly relies on Newtonian mechanics to simulate the motion of the molecular system to extract samples from systems composed of different states of the molecular system, thereby calculating the configuration integral of the system, and further calculating the system based on the results of the configuration integral. Thermodynamic quantities and other macroscopic properties. It solves the equation of motion for a multibody system composed of nuclei and electrons. It is a computational method that can solve the system dynamics problem of a large number of atomic compositions. It can not only directly simulate the macroscopic evolution characteristics of a substance, but also agree with the test results. Similar calculations can also provide a clear image of microstructure, particle motion, and their relationship to macroscopic properties, providing powerful technical support for the development of new theories and concepts.
The object of molecular dynamics is a particle system. The interaction between atoms in the system is described by the potential function. Therefore, the correct selection of the type of potential function and its parameters plays an important role in the simulation results. In most cases, the potential energy function simplifies the description of the geometric deformation of the molecule to the extent that only the simple harmonic term and the trigonometric function are used; instead of the interaction between the bonding atoms, only the Coulomb interaction and the Lennard-Jones potential are used. Combined to describe. Among them, the description of the interaction force between atoms is usually empirical or semi-empirical, which can improve the computational efficiency, but can not fully reveal the multi-body properties of electron bonding, especially the complexities related to its structure and chemistry in the vicinity of defects. Self-consistent variational function. The EAM (Embedded-atom model) potential function of Daw and Baskws combines the multi-body properties of electronic bonding to some extent.
The reliability of the potential function depends mainly on the accuracy of the force field parameters, and the force field parameters can be obtained by fitting experimental observation data and quantum mechanical ab initio data. At present, the most widely used molecular force field in the simulation of biological macromolecular systems is the CHARMM force field and the AMBER force field, which is the molecular force field for the early study of biological macromolecules. Existing force field parameters are still being continually optimized and the types of molecules covered are also expanding. The coarse-grained model is gaining more and more attention in computational biophysical research, since coarse granulated particles are defined in this model, corresponding to several atoms or atomic groups or even molecules in the all-atom model. The number of particles in the system is reduced, so that the time and space scale of the simulation can be greatly improved, but the atomic details will also be lost. Molecular dynamics simulations based on this model are suitable for studying slow biological phenomena or biological phenomena that depend on large assemblies.
The fundamental principle of designing a basic force field is to minimize the computational energy overhead in a time step to maximize the simulation scale. This is especially important for the full atomic force field, even for the so-called coarse grained model. In particular, this principle is extremely important if you want to simulate microsecond or even millisecond time scales.
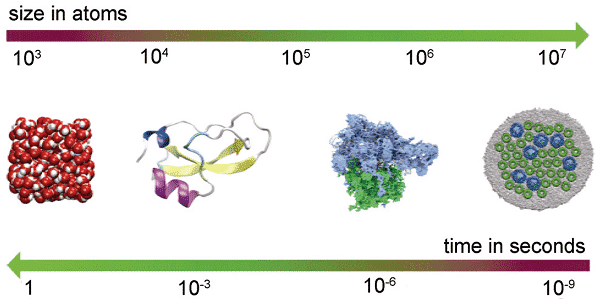
Figure 1 shows the inverse relationship between the time and space dimensions of molecular dynamics, from left to right in the figure: (1) water, the basic components of the cells; (2) bovine trypsin inhibitor, an enzyme, which " Breathing behavior can be examined on a millisecond time scale; (3) ribosomes, a complex biological device that can decode genetic information and produce proteins; (4) purple bacterial photosynthetic membrane fragments, with 25 million atoms, The figure shows the light-harvesting complex embedded in the phospholipid bilayer and the photochemical reaction center .
Figure 1 Scale relationship between time and space of classical molecular dynamics
With the rapid growth of computer processors and the development of massively parallel computing architectures, the combination of massively parallelized or proprietary architecture techniques with scalable molecular dynamics programs, computer simulations range from dislocations to grain boundary-based deformation mechanisms. The entire range of grain sizes opens up new avenues for exploring the research frontiers of materials systems.
For example, William Gon?alves et al. used the Wolf BKS (van Beest, Kramer and van Santen) potential function to describe the interaction between atoms, using the large-scale atomic/molecular parallel simulator LAMMPS (Large-scale Atomic/Molecular Massively Parallel). Simulator) studied molecular dynamics of the elasticity and strength of silica aerogels. They used the velocity-Verlet algorithm and 1.0 fs time step, and used periodic boundary conditions in all three directions.
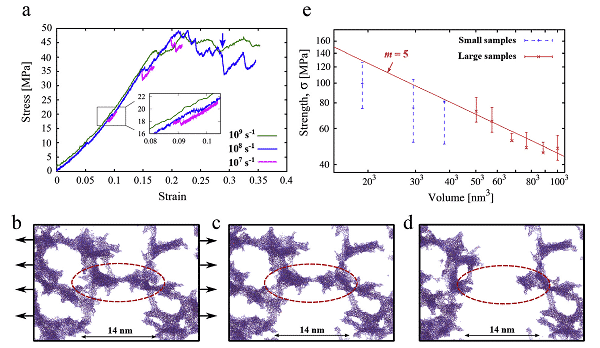
Figure 2 is a 3D schematic diagram of a simulated large volume sample of more than 7,000,000 atoms, and a 20 nm thick sample section and a partial enlarged view (blue is an oxygen atom, red is a silicon atom), and Figure 3 (a) is a 803 nm 3 aerogel. The sample was subjected to a uniaxial tensile test to obtain a stress-strain curve of 300 K, (bd) is a typical ductile fracture image, and (e) a logarithmic relationship between tensile strength and sample volume. They analyzed that in order to ensure proper evaluation of mechanical properties such as elasticity, the size of the simulated sample is at least 8 times the pore size, while the silica aerogel with a positive surface height requires a relatively low strain rate to ensure quasi-static conditions.
Figure 2 Simulated silica aerogel sample (more than seven million atoms)
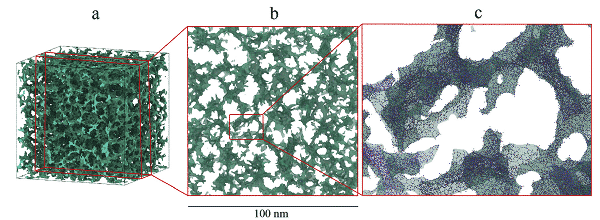
Fig. 3 Stress-strain curve (a), strength-volume relationship (e) and fracture image (b-d) of uniaxial tensile test
Generally, the critical grain size dc is about 20-30 nm, and the larger deformation for the grain size (50-100 nm) is mainly determined by dislocations; when the grain size is less than 30 nm, it is mainly dominated by the GB deformation process, and the grain size is reduced. This results in a decrease in strength and flow stress, ie an "anti-Hall-Petch effect". However, the extensive comparison between multibody and pair potentials used to model GBs in fcc and bcc metals reveals that there is little qualitative difference in the behavior predicted by these different force descriptions, suggesting that multibody effects may not dominate GB behavior.
Bejaud, J. Durinck et al. used molecular dynamics simulation to study the interaction between deformed twins and nanostructured Cu / Ag interfaces, and analyzed the effects of interface structure on the nucleation, expansion and thickening of twins, and explained the mismatch interface. The role of the dislocation grid. Figure 4 shows the Shockley partial dislocation grid (highlighted by black lines), the triangular pattern (white section), and the stacking fault distribution at the interface. Among them, the atom is colored according to the central symmetry parameter, the blue atom is in the perfect FCC environment, and the red atom is in the stacking fault or the twinning fault.
Figure 4 (a) Top view of Cu and Ag atoms along the interface: (ai) COC interface, (a.ii) TO interface, (b) side view along X = <011> direction: (bi) in COC In the interface and the case, the coherent region alternates with the inherent stacking fault (ISF) region, (b.ii) the TO interface, and the double defect region continuously exists in the Cu layer and the Ag layer.
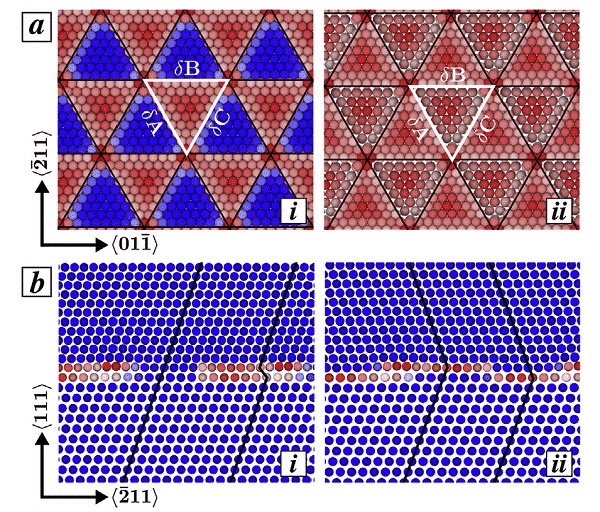
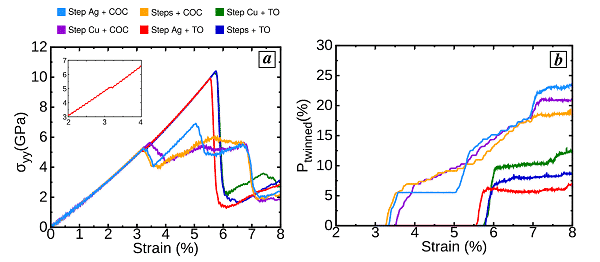
Figure 5 shows the stress-strain curve and the atomic ratio of twins as a function of strain. Through analysis, they found that the interface can directly or indirectly induce nucleation of twin dislocations through Lomer dislocations, and how the heterogeneous interface structure affects the different steps of the mechanical twinning process, thereby affecting the formation of tantalum in the nanostructured Cu / Ag. The size of the crystal. This atomic scale method provides some useful theoretical basis for the mechanical twinning process in nanoscale composites.
Figure 5 (a) stress-strain curve, (b) atomic ratio of twins as a function of strain
Designing multilayer materials to adjust mechanical properties is a hot topic while controlling the deformation mechanism because twinning allows for the incorporation of mechanical properties of nanolayers and nanocrystalline materials. In this regard, this study provides the key to understanding the mechanism of the dual interface interaction and supports the view that heterophasic interfaces promote twinning.
For ultra-fine-scale layered composites containing low-symmetry hcp structural metals, a large number of heterointerfaces can effectively absorb defects such as vacancies and interstitial atoms caused by nuclear irradiation, and hcp metals themselves have low density, specific strength and In recent years, hexagonal multilayer materials composed of Ti, Zr, Mg and other metals have begun to attract people’s attention due to their high specific rigidity and good electrical and thermal conductivity. However, compared with fcc and bcc metals with high crystal structure symmetry, hcp metal has poor room temperature plastic deformation ability, which restricts the use of related composite materials.
In addition to the spatial and temporal resolution of the atomic scale, molecular dynamics simulation can describe the behavior of the fully characterized idealized nanocrystal model, such as interfacial structure, driving force and atomic mechanism; on the other hand, it can be at very high grain boundaries and positions. The large plastic deformation behavior was observed at the wrong density. For example, dislocation nucleation mechanism, grain boundary quenching, mechanical twinning in nanocrystalline Al, reduction of grain size from dislocation to grain boundary-based deformation mechanism, observation of shear band and its fracture surface relationship.
In addition, in the practical application and research process, the theoretical model for different problem descriptions and selections, the dynamics has developed a lot of theoretical branches, for example, Jian Han, Spencer L. Thomas of the University of Pennsylvania and others rely on the power of the boundary The description of the disconnection summarizes the concept of grain boundary dynamics of polycrystalline materials, Zheng Ma et al. studied the precipitation kinetics of FeCO3, as well as surface/interface kinetics.









