The first principle is actually a philosophical term put forward by the ancient Greek philosopher Aristotle: there is a basic proposition in each system, which cannot be violated or deleted.The first principle is actually a philosophical term put forward by the ancient Greek philosopher Aristotle: there is a basic proposition in each system, which cannot be violated or deleted.
Figure 1 Aristotle

In the field of materials science, the first principle refers to the principle of atomic nucleus and electron interaction and its basic motion law. Using quantum mechanics, from the specific requirements, after a series of approximations, the Schrodinger wave equation is directly solved to obtain the electronic structure. Thereby the physical and chemical properties of the system are accurately obtained, and the state and properties of the microscopic system are predicted. However, the solution process is very difficult. For this reason, Born-Oppenheimer proposed an adiabatic approximation, which is to consider the whole problem into the motion of electrons and nuclei. Considering the movement of the nucleus at the instantaneous position, considering the movement of the nucleus, the electron is not considered. The specific distribution of space. For N electron systems, the solution is still very difficult, so a single electron approximation is proposed, that is, only one electron is considered, and the other electrons are treated similarly to some form of potential field, which is converted into a single The electronic problem is the mean field approximation [1, 2].
The first principle is to solve the Schr?dinger equation describing the motion law of microscopic particles by self-consistent calculation on the basis of adiabatic approximation and single electron approximation. The Hartree-Fock approximation is a kind of mean field approximation that ignores the interaction between electrons and treats electrons as movements in the average potential field of the ion potential field and other electrons. The approximation limits the accuracy of the calculation. In 1964, Hohenberg and Kohn proposed density functional theory, which subtly expresses the exchange-related potential between electrons as a form of density functional, so that the properties of the material can be determined from the electron density. Since then, Kohn and Sham (Shen Lujiu) have obtained the single-electron equation in the density functional theory, namely the Kohn-Sham (KS) equation, which makes the density functional theory practically applied [3, 4]. This article summarizes the latest application progress of the first principles in the following aspects:
Calculation of crystal structure parameters and configuration
Crystal structure is the basis for understanding the most basic properties of materials, especially for revealing the relationship between the microstructure of materials and the intrinsic properties of elasticity, electrons, phonons and thermodynamics.
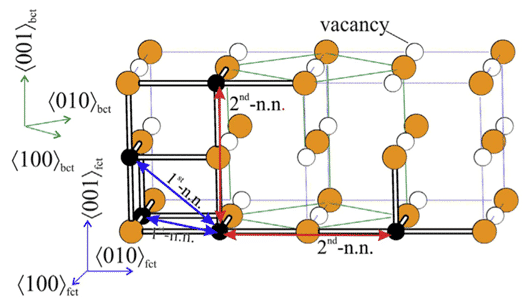
Leineweber and T. Hickel et al. used the exhaustive method to perform DFT calculation on the possible structures of Fe4N and Fe4C, considering the fcc arrangement of Fe atoms and the position of N/C atoms on octahedrons, where part of the structure can pass Bain. The distortion becomes stable, and the C atom exhibits a Zener-type sequence in bcc, as shown in Fig. 2, and reveals the characteristic difference of the orientation tendency of interstitial atoms, which is consistent with the experimentally observed austenitic structure difference [5].
Figure 2 fct (face-centred tetragonal) arrangement of two Fe atoms (blue)
Calculation of alloy phase stability
The first-principles total energy method based on the super-potential plane wave is used to study the crystal phase structure, and the thermodynamic stability of the microstructure of different stacking orders is obtained, so that the most stable structure that may exist is predicted to be a new design and development. An important means of materials.
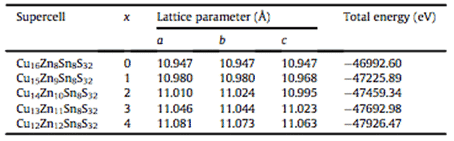
For example, Zhilin Li, Chunyang Xia et al. conducted a first-principle study on the phase stability of Cu2ZnSnS4, a thin-film solar cell absorber layer material, based on density functional theory (DFT), using PBE under generalized gradient approximation (GGA). The lattice parameters and total energy of Cu-Zn-Sn-S alloy system were calculated by exchange correlation potential, and the calculation model and generation energy of possible phases in Cu-Zn-Sn-S alloy were established. The results are shown in Fig. 3 and Table 1. As shown, this study provides guidance for the design of Cu-Zn-Sn-S alloys for thin film composite solar cells. The model and calculation method can also be extended to phase stability prediction of other alloy systems [6].
Fig.3 Superlattice structure model of 64 ZnCu substitution defects
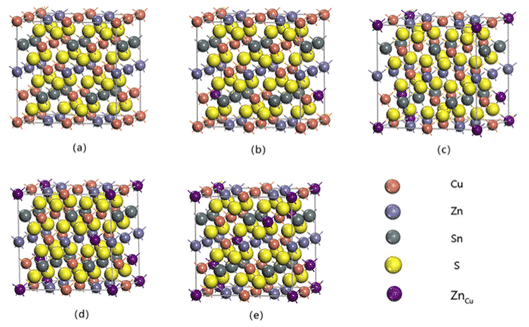
Table 1 Optimized superlattice structure and calculation results of total energy
Electronic structure
For stable structures, calculating the valence electron density distribution of materials is important for understanding the degree of bonding and ionization between atoms.
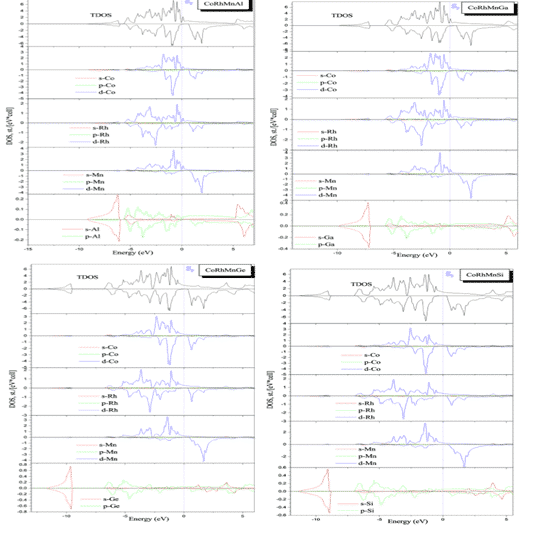
Benkabou and H. Rached et al. used the first principle to calculate quaternary CoRhMnZ (Z = Al, Ga, Ge and Si) Heusler alloys (a class of intermetallic compounds, which can be described as X2YZ or XX0YZ, where X, X0 and Y Is a transition metal element, Z is a group III, IV or V element, generally contains non-ferromagnetic elements, but the compound exhibits ferromagnetic) electronic structure, calculated using the full potential linear affixed plane wave method (FLAPW) and GGA-PBE approximation. Figure 4 shows the results of state density calculations for the corresponding structures, showing that these compounds exhibit semi-metallic ferromagnets in a few states, CoRhMnGe and CoRhMnSi compounds and their magnetic moments are basically consistent with Slater-Pauling’s law, indicating their semi-metallic properties. High spin polarization, in addition to CoRhMnSi, these compounds are stable in the YI structure [7].
Fig. 3 Total density and local density of states of CoRhMnZ (Z = Al, Ga, Ge and Si) stable structures
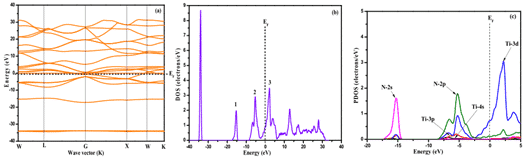
Song et al. used the first principle to study the electronic structure of the TiN film. As shown in Figure 4, the band was simulated by the Studio Studio (MS) program, and the total density of states (DOS), dielectric function, and absorption were calculated. And reflectivity.
The results show that Fermi energy (EF) passes through the energy band with dense energy level distribution, and the total density of states intersects with EF, indicating that TiN is determined by the electronic properties of Ti-3d state to have metalloid properties [8].
Fig. 4 Energy band structure of TiN film (a), full density (b) and local density (c)
Calculation of mechanical properties
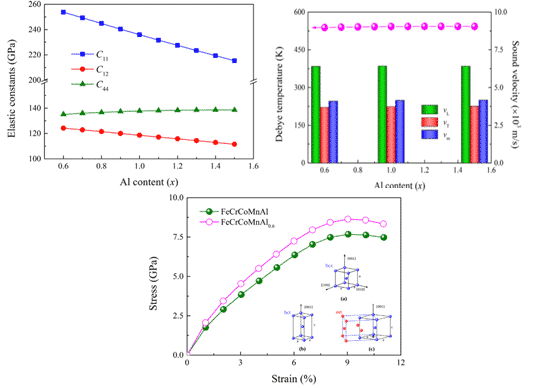
The elastic constant Cij is a basic parameter describing the mechanical properties of materials. It is closely related to basic solid phenomena, such as interatomic bonding, state equations and phonon spectra, as well as thermodynamic properties such as specific heat, thermal expansion, Debye temperature and Grüneisen parameters. Related. Theoretically, there are 21 independent elastic constants Cij, but the symmetry of the cubic crystal reduces this value to only 3 (C11, C12 and C44), and the shear modulus G, Young’s modulus E and Poisson are derived from the elastic constants. Ratio n, then estimate the Debye temperature from the average sound velocity Vm:
Where H is the Planck constant, KB is the Boltzmann constant, Va is the atomic volume, and Vm can be determined by the longitudinal and lateral sound velocities vl and vt obtained by the shear modulus G and the bulk modulus B in the Navier equation. .
For example, Shuo Huang et al. combined the first principle to determine the elastic parameters and ideal tensile strength of the FeCrCoMnAlx (0.6≤≤1.5) high-entropy alloy body-centered cubic solid solution phase in the [001] direction. The results are shown in Fig. 5. Within the compositional range considered, the bcc structure was found to have lower energy than the ferromagnetic and paramagnetic states of the fcc and hcp structures. Based on the theoretical Curie temperature, all alloys are expected to be ferromagnetic at room temperature, and the ideal tensile strength in the [001] direction is expected to be 7.7 GPa at a maximum strain of about 9%. The strength can be further increased by lowering the Al concentration. [9].
Fig.5 Elastic constant, Debye temperature and stress-strain curve of FeCrCoMnAlx high-entropy alloy
Calculation of surface or interface properties
Recently, Yu Lu et al. used Sn9Zn-1Al2O3-xCu composite brazing filler metal to braze 6061 aluminum alloy, and studied the effect of adding Cu element and Al2O3 particles on brazing performance. Based on the theory of density functional theory (DFT) and GGA-PBE, the first-principles calculations were carried out on the interfacial structure, interfacial energy, contact angle and electronic properties of Al2O3/Sn9Zn. The calculations show that Sn9Zn-1Al2O3-4.5Cu and Sn9Zn-1Al2O3-6Cu has a stable structure, and the corresponding results are shown in Figures 6 and 7 [10].
Figure 6. Contour planes with different charge density differences for different structures:(a)Sn9Zn—1Al2O3,(b)Sn9Zn—1Al2O3-4.5Cu
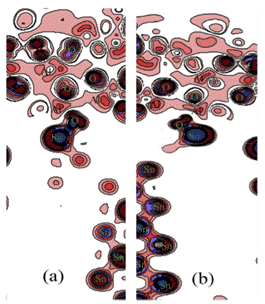
Figure 7 Localized state density of different structures:(a)Sn9Zn-1Al2O3, (b) Sn9Zn-1Al2O3-4.5Cu

Other applications
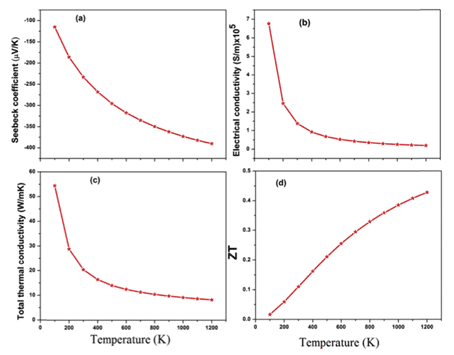
For example, Kulwinder Kaur et al. used density functional theory (DFT) and Boltzmann transmission theory to study the high-temperature thermoelectric properties of fcc HfRhSb. Figures 8 and 9 show the calculated energy band structure and density of states, as well as some physical parameters. The theory of transmission characteristics begins with the calculation of the band structure, the Boltzmann transmission theory in the rigid band and the constant relaxation time approximation (RTA). Rigid performance band approximation (RBA) is an effective tool to study the relationship between band structure and thermoelectric response [11].
Figure 8 (a) energy band structure (b) full, local state density (c) phonon dispersion (d) phonon DOS
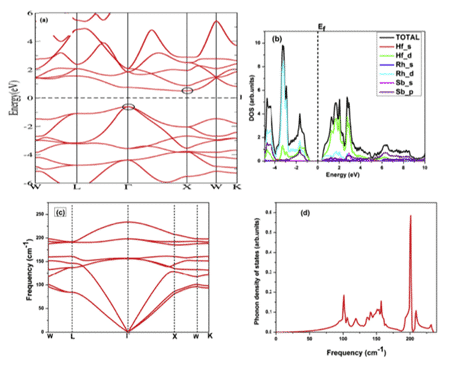
Figure 9 Seebeck coefficient, conductivity, thermal conductivity and thermoelectric efficiency ZT as a function of temperature
Odniesienie
1.Heisenberg W. Quantum-theoretical re-interpretation of kinematical and mechanical relations [J]. Z Phys, 1925, 33: 879
2.Schrodinger E, Quantisierung als eigenwertproblem I [J]. Ann der Phys, 1926, 9: 361
3.Hohenberg P, Kohn W. Inhomogeneous electron gas [J]. Phys Rev B, 1964, 136(3): 864
4.Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects [J]. Phys Rev A, 1965, 140(4): 1133
5.Leineweber, T. Hickel, B. Azimi-Manavi, S.B. Maisel,Crystal structures of Fe4C vs. Fe4N analysed by DFT calculations: Fcc-based interstitial superstructures explored [J], Acta Materialia 140 (2017) 433-442
6.Zhilin Li, Chunyang Xia, Zhengping Zhang, Meiling Dou, Jing Ji, Ye Song, Jingjun Liu, Feng Wang,F(xiàn)irst-principle study on phase stability of kesterite Cu2ZnSnS4 for thin film solar cells with off-stoichiometric composition [J],Journal of Alloys and Compounds 768 (2018) 644-651
7.Benkabou, H. Rached, A. Abdellaoui, D. Rached, R. Khenata, M.H. Elahmar, B. Abidri, N. Benkhettou, S. Bin-Omran,Electronic structure and magnetic properties of quaternary Heusler alloys CoRhMnZ (Z=Al, Ga, Ge and Si) via first-principle calculations [J],Journal of Alloys and Compounds 647 (2015) 276-286
8.Huijin Song, Peng Gu, Xinghua Zhu, Qiang Yan, Dingyu Yang,Study on the electronic structure and optical properties of TiN films based on the first-principle [J],Physica B: Condensed Matter 545 (2018) 197–202
9.Shuo Huang, Xiaoqing Li, He Huang, Erik Holmstro€m, Levente Vitos, Mechanical performance of FeCrCoMnAlx high-entropy alloys from first-principle [J], Materials Chemistry and Physics 210 (2018) 37-42
10.Yu Lu, Le Ma, Shu-yong Li, Wei Zuo, Zhi-qiang Ji, Min Ding,Effect of Cu element addition on the interfacial behavior and mechanical properties of Sn9Zn-1Al2O3 soldering 6061 aluminum alloys: First-principle calculations and experimental research [J],Journal of Alloys and Compounds 765 (2018) 128-139
11.Kulwinder Kaur, Ranjan Kumar, D.P. Rai, A promising thermoelectric response of HfRhSb half Heusler compound at high temperature: A first principle study [J], Journal of Alloys and Compounds 763 (2018) 1018-1023









